大阪星光学院　２０１５年度　算数（その２）

２０１５大阪星光学院中学校の算数は難しい？

大阪星光学院の公式サイトに、今年２０１５年度の入試問題がアップされています。

問題の紹介と、解いてみた感想を一言。（一応、難易度をＡ･･･易しい，Ｂ･･･やや難，Ｃ･･･難　としました。あくまで主観です　m(__)m　）

２枚目に入ります。

大問３はよく見かける速さシリーズ

星光の入試問題でよく見かける速さシリーズなんですが、今回のは簡単です。

A，B，Cの3人がＸ地点とＹ地点の間を往復する競走をしました。3人同時にＸ地点を出発し，AはＹ地点まで行って1.5km折り返してきたところでＹ地点に向かうBと出会い，そこからさらに1.5km進んだところでＹ地点に向かうCと出会いました。AがＸ地点に戻ってきたとき，BはＸ地点まであと5kmのところにいました。3人の速さはそれぞれ一定であったとして，次の問いに答えなさい。

(1)　AとBの速さの比を最も簡単な整数の比で表すと□：□です。

(2)　Ｘ地点とＹ地点の間の距離は□kｍです。

(3)　BとCの速さの比を最も簡単な整数の比で表すと□：□です。

状況図を描き、それをしっかり見つめて解答を作っていきましょう。

（１）「AはＹ地点まで行って1.5km折り返してきたところでＹ地点に向かうBと出会い」ここから、AとBの進んだ距離の差は１.５×２＝３ｋｍと分かります。（㋐）

「AがＸ地点に戻ってきたとき，BはＸ地点まであと5kmのところにいました」ここから、AとBの進んだ距離の差は５ｋｍです。（㋑）

㋐，㋑の２つより、〔出発してからAとBが出会うまでの時間〕：〔出発してからAがＸに戻るまでの時間〕＝３：５と分かるので、その時進んだ距離の比も３：５になります。

このことからAとBが出会うまでにAの進んだ距離とBの進んだ距離の比が３：２と分かるので、速さの比も３：２となることが分かりますね。

この問題ができて、状況図に必要な数字を書き込んでいくことで（２）や（３）はた易くできてしまいます。ちなみに（２）は７.５ｋｍ，（３）は１４：９です。

難易度は（１）Ｂ，（２）Ｂ，（Ｂ）

（注　(1)が解けていれば(2)(3)はAレベルです。）

大問４は反射の問題ですが･･･

星光を狙っている受験生なら、反射の問題の練習は十分積んできたことと思います。

このタイプの反射の問題は定石通り手を打てば勝手に解答が出てきますね。

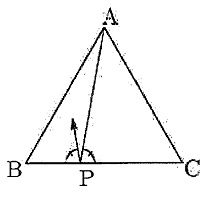
正三角形ABCがあります。頂点Aから辺BC上の点Pに向けて発射された球は，右の図のように反射して辺ABまたは辺ACに当たります。球はこのような反射をくり返し，いずれかの頂点に到達したときに止まり
ます。球の大きさは考えないものとして，次の問いに答えなさい。

(1)　反射の回数が3回となるような点Pの位置は□か所あります。

(2)　反射の回数が7回となるような点Pの位置は□か所あります。

(3)　反射の回数が9回となるような点Pの位置は□か所あります。

この問題は「鏡の世界」で考えると1発で正解できます。

△ＡＢＣをＢＣで裏返した図を描けば、Ａから出た球をまっすぐ進めることができます。

三角形を次々と裏返して描き、横切る線の数を反射した回数と考えればいいわけです。

慎重に作図ができればあとは数えるだけ。

（１）は２通り、（２）は４通り、（３）は２通りとなります。

難易度は、「鏡の世界」の方法を知っていれば、（１）Ａ（２）Ａ（３）Ｂというところでしょう。

大問５に続きます。

算数の入試問題のレベルを知るに戻る