算数教え方講座～平面図形

平面図形の出題率は問題全体の4分の1程度

大体の難関校の算数入試問題を見てみると、おおよそ4分の1は平面図形がらみの問題で、これ自体は多すぎず少なすぎずという感じです。

ですが、この平面図形に苦手意識があると、合否に決定的な差をつけられてしまいます。

単純に公式を使って面積を求めるというような問題は「皆無」、たいていは、面積を求めるにしろ、「比」をきちんと使えないと話になりません。

2018年度大阪星光の大問３では

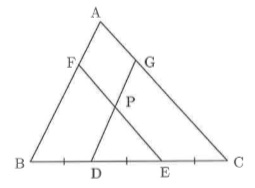
図は、大阪星光で2018年度に出題されたものです。

点D，Eは辺BC＝12cmの3等分点。DGもEFも三角形ABCの面積を2等分する、というもの。

ここで、AFとFBの比を求めたり、FGの長さを求めたり、三角形ABCと三角形PDEの面積の比を求めたりしないといけません。

難問ではないですが、ふだん取り組んでいる「平面図形と比」の基本をきちんとやっていないと、正解にはたどり着けません。

➤　解法の一つをごくごく簡単に書けば

三角形ABCと三角形PDEの面積の比は、BA×BC：BF×BE＝2：1

これよりBA：BF＝4：3が分かり、同様にCA：CG＝4：3が分かります。

これをクリアすれば、この問題は簡単ですね。

難関中学の平面図形に対応する力って、どうやってつけたらいい？

では、このような難関中学で出題される問題への対応力はどうつけるのか。

正解は「とにかく基本をおさえる」こと。

基本公式はもちろん超重要なので、しっかり暗記させましょう。
正方形、長方形、三角形、平行四辺形、ひし形、台形。
ですが、これも、ただ覚えるだけでは使いこなせません。

底辺と高さの関係を、具体的につかむ必要があります。

特に三角形。
基本図形をいくつも見せて、底辺と高さの関係を体で覚えさせましょう。
具体的な「高さ」のイメージをつかめるようにするには、次のような例えがいいかもしれません。

三角形を、底辺を下に置いて、斜めになった辺をてくてく歩いて上まで上ります。
手にリンゴでも持っておきましょう。
一番高いところまで来たら、持ってきたリンゴを落とします。
リンゴは底辺の方に向かって、まっすぐ落ちていきます。
そのときリンゴが落ちた長さが「高さ」です。
そして、落ちるときには、地面(底辺)に垂直に落ちていきますから、そこに直角マークがつきます。

ですから、直角マークがついていたら、それは「高さのしるし」です。
高さの感覚が身に付いていないと、とりあえず２つの数をかけて、２で割っておこうということになってしまいます。

３.１４と約分

おうぎ形の弧の長さを求めたり、面積を求めたりするとき、小学校では３.１４の計算を避けては通れません。(入試問題では、学校によっては３.１４ではなく、$\frac{7}{22}$ を使わないといけないところもあります。)
とにかく、徹底的に約分をやって、最終的には
□×３.１４
という形に持ち込むこと。

３.１４の計算はできるだけまとめる。

たとえば

12×3.14＋24×3.14－6×3.14だったら
(12＋24－6)×3.14

とすれば、3.14の計算は1回だけで
30×3.14とできます。

こうすることで、計算ミスも減り、スピードもアップします。

比がからむ図形の問題も、とても大切。

先に挙げた大阪星光の入試問題も、とにかく「比」がメインテーマ。

相似、底辺の比と面積の比、隣辺比などなど。

特に「比を利用して解く」図形の問題は、所属している塾によって、教え方が変わってくる部分が多いところですが、そこで教えられた「基本」に忠実に解いていけば、かなり難しい（と感じるような）問題でも、きっと解法は見つかるはずです。

徹底的に基本を身につける、これに勝る方法をボクは知りません。

「基本を身につける」ための学習方法

塾だと、結構多くの問題に触れさせて、身をもって問題に馴染ませる、ある程度大量に問題を解かせるのはやむを得ないことだ、という前提で、やたらめったらたくさん問題をこなさせるところも多いですよね。

それはそれで一つのやり方だし、もちろん歯をくしばってついていけば力もついてきます。「習うより慣れよ」ですね。

ですが、睡眠時間も削り、体力をすり減らしながらギリギリの状態に追い込まれてしまって、授業中に頭がぼーっとしてしまったら本末転倒です。

そこで、ボク管理人からのおすすめの勉強方法をひとつ書いておきます。

それは、「数をこなしながら理解していく」のではなく、「理解してから数をこなす」という方法です。

たとえば、使っている教科書から、類題、基本問題、応用問題、発展問題の宿題が出たとします。

まず「例題」「類題」の考え方、ポイントは確実に理解してから基本問題に取り組みます。

どの段階でもそうですが、自分では分からない、というとき、

次の授業で先生に質問する、でもいいのですが、
それだと質問できるまでの時間がかかりすぎです。

そこで、

「解説を理解する」という方法も身につけましょう。

解説を理解できるには、そこに書かれたことを徹底的に分かろうとする姿勢が大切です。

これをすることで、徐々に実力も身につきます。

子供たちの混乱しやすいことにも注意しよう

相似な図形では、面積比は相似比の２乗に等しい、と習うのですが、これを高さが等しい三角形の面積比に使ってしまう。
こういう子が、一定数います。

相似は、形が全く同じことだよ、といくら言っても、彼ら、彼女らの頭の中では、しばらく混乱が続きます。

これを防ぐひとつの方法は、これも、とにかく、図をかく。

図形の問題では、教科書にしっかりした図が載っていることが多く、大抵の子は、自分で図をかかず、教科書の図にどんどん書き込みをして考えるようです。
中には、テキストを汚すとママに叱られるからと、せっせと書き込んだことを消しゴムで消している子もいます。

ボクからの提案は、とにかく、下手でも何でもいいので、ノートに図を写してから問題を解くようにすること。

図を写す過程で、問題に書かれた条件をよりきちんと把握できるし、それを図に書き込んでいくことで、問題を解くためのヒントが図の中に出来上がっていく。

ボクが問題を解く際は、特に初見の問題であれば、この作業は欠かしません。

算数教え方講座に戻る