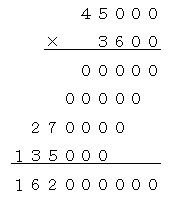計算力が算数の土台をつくる

計算力が算数の土台をつくるってホントです!
たかが計算、されど計算・・・
算数を教えていると、子供たちの計算力の低さに驚くことがあります。
今まで遭遇した極端な例は、例えば
・12+7をひっ算でする
・36×10をひっ算でする
・2.8×4500のひっ算を、後ろの数字8と0をそろえて書く
(こんなふうになってしまいます。)
列をそろえて書けているならまだしも、縦に伸びる分、答えのところでずれてくることも多く、百害あって一利なしですよね。
速く正確に計算できる方法を身につけさせてほしいです。
今はどうかわからないけど、昔の小学校で、次のようなひっ算を書かせている方がいて、修正するのに難儀したこともあります。
指導した先生は、おそらくですが、位取りを正しく教えないといけないという使命感から、こうされたのでしょうが、
小学校の教科書に出てくる問題なら、百歩譲って、仕方ないなと思えるかもしれません。
ですが、
230000×50000000
こんな問題でも、同じように教えるのでしょうか。
正確に速く計算ができるメリット
ちょっと極端な例を取り上げましたが、ここまでひどくなくても、わが子を見ていて、
”うちの子、ちょっと計算がどんくさいわ・・・”
とお感じになった方もいらっしゃると思います。
問題を解いている途中で、「それぐらい、暗算でやってよ!」みたいな計算を、いちいちひっ算でやったり、
下手をすると、3年や4年になっても「指を折ってやってる」ことも。
計算が遅いと、思考の流れが分断されます
ちょっと複雑な問題を解いているとき、計算のところでその都度立ち止まっていたら、
思考の流れが分断されてしまって、
計算の答えが出たときに、
「あれ? 今、何をやってたっけ?」
となりがちです。
せっかくいい方向で考えていたものが、計算が遅いばかりに、答えに行きつかない、なんてことも実際あります。
答えの予想ができます
また、問題を考えていくとき、概算で、だいたいこんな答えか・・・と予め予想できていたら、
間違った方向に進む前に、思考の向きを修正できたりもします。
ですから、少なくとも、流れを止めない計算力は身につけておく必要がありますね。
ひっ算に頼り過ぎない
複雑な計算は、もちろんひっ算を書いて、きちんと答えを求めないといけません。
ですが、先にも書いた通り、途中の計算に時間をかけてしまうと、
思考の流れが分断されて、自分の向かっている方向が分からなくなってしまうこともあります。
ですから、少なくとも
・2けたどうしの足し算や引き算
・2けたや3けた×1けたのかけ算
これぐらいは、暗算でスムーズに求められるように、日ごろから練習を積んでおきたいところです。
できれば、
・2けたや3けた÷1けた
も暗算で出来てほしいところです。
暗算力をつけてほしい
こういった計算がスムーズにできるようになってくれば、
約分や通分、約比などもすらすらできるようになってきます。
(約分の際、分母・分子を2で約分するのに、「ひっ算する」なんて、あり得ません。
ですが、実際そういう子はいます・・・)
ひっ算をやったらだめ!とまでは言いませんが、ある程度の計算は、暗算で求められるようになっておきましょう。
簡単な暗算の公式
25×4=100だとか、125×8=1000だとかを使って、
32×25=8×4×25=8×100=800とか、
56×375=7×8×125×3=21000とかを求めることはできます。
これもできてほしいです。
ですが、ここではもっと単純な
・2けた+2けた=3けた
・3けた-2けた=2けた
これを暗算でやる「公式」を紹介します。
・2けた+2けた=3けた
まず、「あといくつで100になるか」を使う方法
87+38だったら、87はあと13で100ですから
先に38のうち13だけを87に渡すと、残りは25です。
式で書けば、87+13+(38-13)=100+25=125
あといくつで100か?がすっと頭に浮かぶ人には簡単な方法です。
次は、ひっ算をバラシて使う方法
87+38なら、80と7と30と8なので、
80と30で110、7と8で15
式に書くと、(80+30)+(7+8)=110+15=125
・3けた-2けた=2けた
137-49だったら、まず37だけ引きます。
137-37=100
ここから残りの(49-37=)12を引けばいいので、
100-12=88
他にも、いろんな暗算の仕方があると思うし、子供が自分で編み出すものもあるでしょう。
子どもがいい方法を考えた!って言ったら、しっかり受け止めてあげて、褒めてあげましょう。
本当にいい方法のこともありますよ。
算数の成績を上げたいにもどる